
Precision in Language
Mathematical Language
Learning mathematical language can be quite challenging. This is because the English language is challenging.
We have
- homonyms – words that sound alike but have different meanings. The spelling could be the same or different. Ex. fair (county fair) vs fair (reasonable). Pear (fruit) vs pair (couple)
- homographs – words that are spelled the same but have different meanings. The sound could be the same or different. Ex. lie (untruth) vs lie (lie down). Tear (in the eye) or tear (rip)
- homophones which are subset of homonym. They are limited to words that have the same sound and different spelling. Ex. Pear (fruit) vs pair (couple)
- Heteronyms which are a subset of homograph. They are limited to words that have different sounds and the same spelling. Ex. tear (in the eye) vs tear (rip)
We use words in math that are
- homonyms/homophones: sum vs some
- homographs/heteronyms: divide, product
Can you think of others?
How often do we use a mathematical word that students are interpreting in a non-mathematical way? This is especially true for additional language learners.
Using Precise Mathematics Language to Engage Students in Mathematics Practice by Adams, Smith Karunakaran, Klosterman, Knott and Ely presents three classroom interactions where the teachers supported students in using precise mathematical language during mathematical discussions. The first interaction focuses on equivalent fractions. The second focuses on “Add a Zero for Multiples of ten”. The third focuses on “add a zero for place value”.
As we learn more about students’ misconceptions and precision in language, we become more precise in the terminology we use. “When we don’t know…we don’t know. But when we do know, we can do better.”
The following are a few examples of imprecise language or statements we make that can cause student misconceptions. You will also find these, and eventually more, on the concept pages.
Numbers:
Take a moment to think about the number 5. What is it? Can you picture it in your head? How would you explain “5” to someone else?
Did you think about a collection of 5? 5 apples? 5 balls? What about the roman numeral V? A number is an abstract representation and can be hard to define.
A “numeral” is what we use to represent 5. A numeral can be any name or symbol used for representation. 17 is the numeral we use to represent the abstract concept of 17. XVII is also a numeral.
When you thought about the number 5, did you think about it as it relates to the numeral 51? Probably not. This is because in the numeral 51, 5 is a digit not a number…nor is 5 a numeral. There are 10 digits in the base ten system. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. When working with students, it’s important to reference the 5 as 5 tens or 50 but not as the number 5. If they see the 5 as the number 5 rather than a digit, it can cause misconceptions when working with addition and subtraction.
Numeral and number are often interchanged though number is the abstract concept and numeral is the symbolic representation. This seldom causes misconceptions. However, interchanging digit and numeral/number can lead to significant misconceptions.
Consider the following solution:
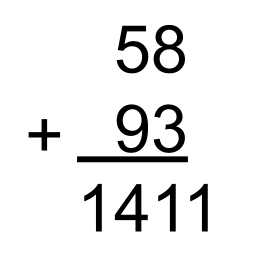
This student may even respond that the final answer is 25 because 14 + 11 = 25.
Why might a student respond in either of these ways? Think about the misconceptions that this student has internalized as a result of the misuse of the terms digit, numeral and number. This student sees the 5 as the number 5 which has a value of 5, rather than the digit 5 which has a value of 50. The same can be said for the digit 9.
It is imperative that students understand the distinction between digits and numerals/numbers.
Equality:
Misconceptions around the equal sign can be aggravated by using the phrase “is the same as”. Phrases such as “is the same number of blocks as”, “is the same value as”, or “is the same total as” are more precise phrases. However, “is the same as” can be misleading. This implies that they are the same, when in fact, they are not. Let’s consider an example from grade 3 to help explore this idea. You would agree that 3 x 4 has the same result as 4 x 3. However, 3 x 4 is not necessarily the same as 4 x 3. For example, 3 dogs with four legs have the same total number of legs as 4 dogs with three legs but it’s NOT the same situation. In both cases, there are 12 legs but the rest is not the same.
Addition and Subtraction Operations:
Consider the following student work. If you had a student solve the question this way, what might you say to the student in order to “fix” the work?
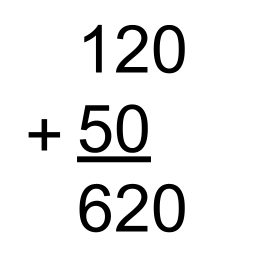
Is that advice helpful or hurtful when it comes to solving the question 4.2+3.75+2?
Did you tell the student to line the numbers up to the right? If so, that statement is hurtful when working with decimals. We don’t line the numbers up to the right. We line the numbers up according to place value. We don’t say “line it up according to the decimal” either. Students often struggle solving addition questions with decimals such as the one above as the 2 “does not have a decimal”. How often do we say, “If it doesn’t have a decimal, just put one in.”? Students need to understand that the decimal is a visual used to separate the whole values from the part values.
Subtraction:
When you are solving a subtraction question where regrouping is required, such as 84-29, we do not “borrow” from the tens place. Think about “borrowing” in real life. If someone borrows something from you, what is the expectation? You expect them to return it. In subtraction, you do not “give back” the 10. The most appropriate phrasing would be regrouping.
A common statement made to younger students is that you “can’t take a bigger number away from a smaller number.” This is undeniably false. We can solve 3-8. The answer is -5. Of course, this is a concept introduced at a higher grade. Students who have not been introduced to negative numbers will interpret the statement “you can’t take a bigger number away from a smaller number” to mean that you then must take “the smaller number away from the bigger number”. When solving a question like 24-19, they end up with 15 because they will start by figuring out 9-4 because you have to take the smaller number away from the bigger number. The 4 is a digit in the numeral 24 and the 9 is a digit in the numeral 19. When considering the numerals 24 and 19, 4 and 9 should never be referred to as numbers.. See notes around number vs numeral vs digit in the “Numbers” section.
References:
Adams, A. E., Smith Karunakaran, M., Klosterman, P., Knott, L., & Ely, R. (n.d.). Using Precise Mathematics Language to Engage Students in Mathematics Practice. Teaching and Classroom Practice, 1158-1165.