Numerate Environment

Learning is more than Just Getting the Right Answer

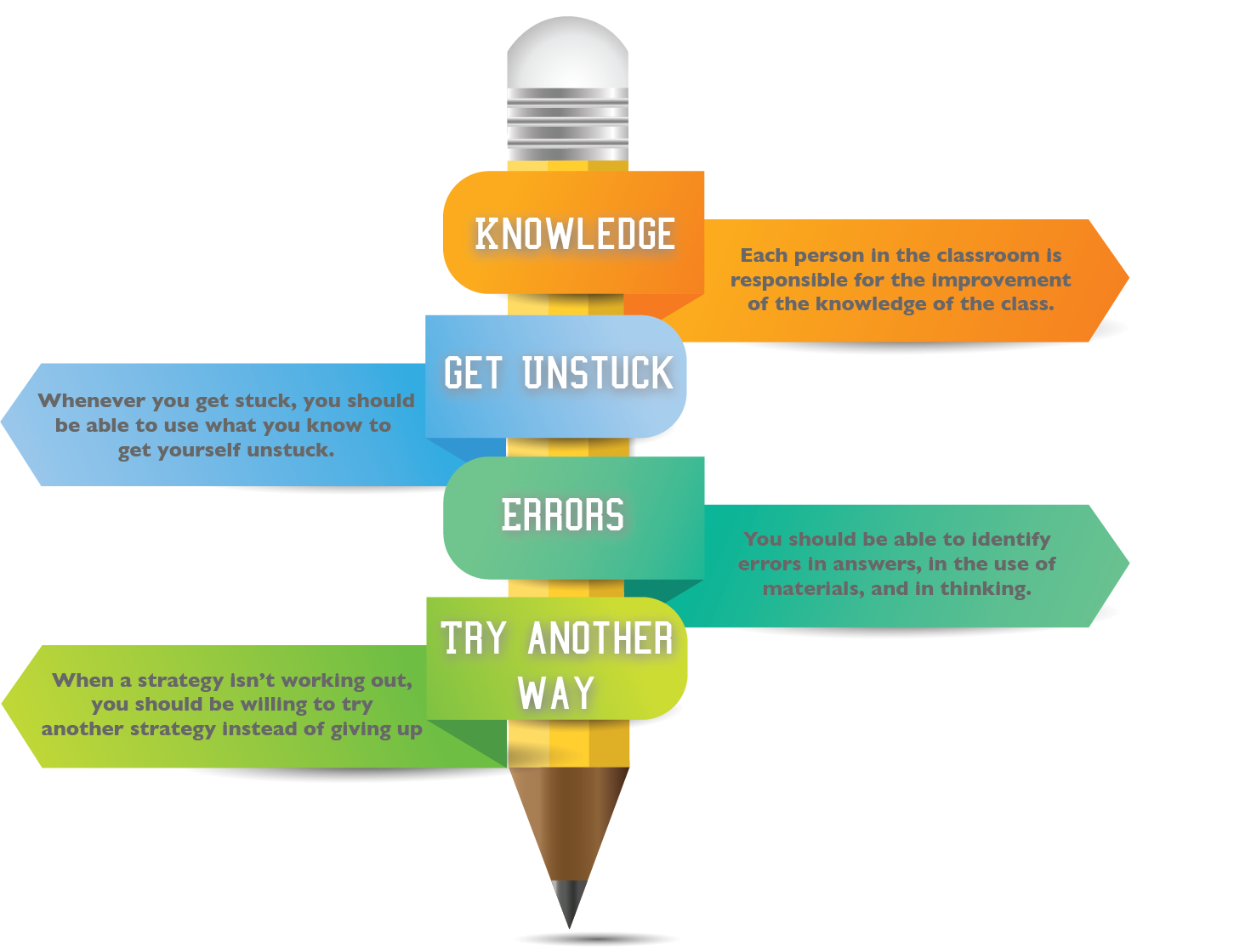
The assumption that correct answers mean mastery and wrong answers mean learning deficiencies needs to be reimagined. The following learning criteria based, on the work of Greenwood (1993), and Middleton, Hatfield & Tallman (2015) challenges students to think beyond just getting the right answer.  The norms found below are designed to be introduced during the first math class of the year. They can be posted (and added to) so they can be referred to daily.

Printable poster for classroom use

How do I Support This?

The examples below are taken from the following source: Making Connections in Math (see bibliography section)

CONSIDER

Each person in the classroom is responsible for the improvement of the knowledge of the class.

Message to your students: “You should be able eto explain your strategies and thoughts so they are clearly understood by others, not just repeat the steps of what to do to get an answer.

• Provide opportunities for students who recognize their difficulties to make their struggle public so others can learn.
• When students have a particular insight, provide opportunities to share the insight publicly to improve the knowledge of peers.
• Asking open-ended and extended-answer questions. After asking the question there should be time given to the students to think of their response. Even after they respond, try to give more wait-time and also ask the students to explain their response. Students should expect probing questions throughout the year so that they begin to see that more will be expected of them that just the correct answer (Greenwood, 1993; NDT).
• Asking students “why-questions” or “what if questions” to encourage students to think more deeply about their responses (NDT; Reinhart, 2008).

Whenever you get stuck, you should be able to use what you know to get yourself unstuck.

• Answering students questions with questions that will provide clues to help them get unstuck without giving them the answer (Greenwood, 1993). 
• Getting student to serve as “strategy teachers.”  Students share with the class the difficulties they encountered and the strategies they used to get unstuck (Greenwood, 1993).
• “Always require student to ask a question when they need help. When a student says, “I don’t get it,” he or she may really be saying, “Show me an easy way to do this so I don’t have to think.” By having to ask a question, students are required to think about the problem in enough depth to formulate a question (Reinhart, 2008, p. 93)

You should be able to identify errors in answers, in the use of materials, and in thinking.

• Asking students whether they agree or disagree with something and whether they can spot some mistake. “If something is wrong and you can spot it, that will tell us both that you know it is supposed to be. If nothing is wrong and you  think there is, that will tell us something too.” (Greenwood, 1993, p. 146; NDT)
• Requiring multiple responses to the same question. “Always ask for other comments, additions, clarifications, solutions or methods.  This request is difficult for students at first because they have been conditioned to believe that only one answer is correct and that only one correct way is possible to solve a problem…To accomplish this…try not to comment after each response…simply pause and wait for the next student to offer comments. If the pause alone does not generate further discussion, …ask, “Next?” Or “What do you think about ______’s idea?” (Reinhart, 2008, p. 93)

Resources to use with your Class and Students:

Children’s Literature Available in IMC

Great Estimations by Bruce Goldstone

Perimeter, Area and Volume (A Monster Book of Dimensions) by David Adler

Reserve Books Now

Online Books