Strategies vs Models
Strategy: How students solve the problem. (Examples: Decomposition, Compensation, Traditional Algorithm)
Model: How students notate their thinking. (Examples: Number line, Ten Frames, Base Ten Blocks)
Important to Know:
One strategy can be explained using multiple models. One model can be used to explain multiple strategies.
Fluency with strategies evolves over time.
The Development of Mathematical Reasoning
Pamela Harris' Development of Mathematical Reasoning: Counting Strategies ⇒ Additive Thinking Strategies ⇒ Multiplicative Reasoning Strategies ⇒ Proportional Reasoning Strategies ⇒ Functional Reasoning Strategies
Students develop mathematical reasoning as they develop more sophisticated thinking. A student who solves 4 x 5 by using counting strategies or additive thinking strategies is not engaging in multiplicative reasoning. Although, this student will correctly determine the answer to 4 x 5 using other strategies, if they do not develop multiplicative reasoning, exploring more complex questions will be extremely challenging. For example, a student may use counting or additive thinking strategies as part of their process for solving 1.2 x 2.3 or (x + 2)(x - 1), but will be unable to solve it without using multiplicative thinking.
When a student develops fluency in multiple strategies and more sophisticated strategies, the student can confidently select the most appropriate strategy based on the numbers.
Naming Strategies:
Mathematical strategies should be named using the math utilized in the strategy. It might be cute to name the strategy after the student who first demonstrates it in class but when a student moves to a different class or a different school, non-conventional naming is not helpful. A grade level team and, preferably, a school, should agree upon names for the strategies that will be explored in math class. There aren't that many of them. Decomposing, compensating, partitioning by place value, give and take, and the traditional algorithm will cover almost all possible strategies.
Strategies for this concept:
Below you will find a short description for each of the most typically used strategies for additive thinking. Each strategy will include one or two models to help notate the thinking within the strategy. When solving a question, a student might use a single strategy or apply two or more strategies. Note that, although the sample question provided below could be solved using other reasoning, only the reasoning appropriate to this concept has been included.
Read about the criteria used to select high leverage strategies.
Examples of both addition and subtraction have been included (when appropriate) for each strategy.
Addition: 243 + 189
Subtraction: 432 – 189
Compensation
Adjust one of the numbers to make it easier to work with while keeping the other number the same. Solve the new question. Adjust the answer to account for (compensate for) the change made to the first number.

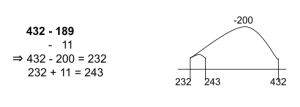
Introducing the strategy for Addition: Google Slideshow
Introducing the strategy for Subtraction: Google Slideshow
Give and Take (Addition)
Similar to compensation but uses more sophisticated thinking. Adjust one of the numbers to make it easier to work with by “taking” that value from the other number. Solve the question using the new numbers.
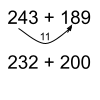
Introducing the strategy: Google Slideshow
Constant Difference (Subtraction)
The difference (distance) between two numbers does not change when you add or subtract the same value from both numbers. “Shift” the numbers to numbers that are easier to work with. Solve the question using the new numbers.
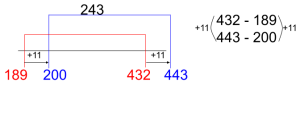
Decomposition
Decompose (break apart) one or both of the numbers into more manageable values in order to make it easier to solve.

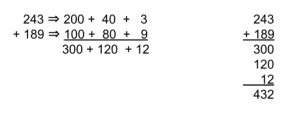
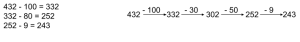

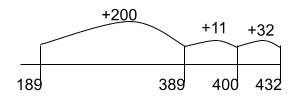
Adding up to find the Difference: (Subtraction)
This strategy focuses on the inverse nature of subtraction. Students are finding the distance between the subtrahend and minuend. The example below starts at the subtrahend and “adds up” to the minuend. However, you could also start at the minuend and “subtract down” to the subtrahend.
Traditional Algorithm
The traditional algorithm (often called the standard algorithm) is a standardized process for solving addition and subtraction questions. It focuses on solving a question digit by digit. Caution: The Traditional Algorithm most often described by Canadians is the traditional algorithm for Canada. Other countries have their own traditional algorithms. Keep this in mind if using this phrasing with students. (Source)
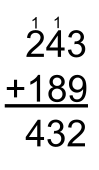
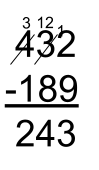
Video Examples
Some videos you might find helpful have been included below.
Pocket Subtraction – when the Minuend ends in Zero
This strategy is useful in subtraction questions where the “starting” number ends in a zero.
The correct name for this strategy is “Compensation”. You change one of the numbers (in this case the minuend), in order to make solving the question easier.
Pocket Subtraction – when the Subtrahend ends in 9
This strategy is useful in subtraction questions where the number that is being subtracted ends in 9.
The correct name for this strategy is “Compensation”. You change one of the numbers (in this case the subtrahend), in order to make solving the question easier.
Adding 2 Digit Numbers – without regrouping
This video is Part 1 of the 2 part series “Addition of 2 Digit Numbers – Partitioning by Place Value”. Part 1 focuses on building and solving 2 Digit Addition questions that do not require regrouping. You will then compare this method to the traditional algorithm.
You will need access to one of the following:
- Physical Base Ten Blocks (tens and ones)
- Printable Base Ten blocks (print in black and white OR color)
- Virtual Base Ten Blocks e.g. CPM Tiles
The correct name for this strategy is decomposing because you are partitioning by place value.
Adding 2 Digit Numbers – with regrouping
This video is Part 2 of the 2 part series “Addition of 2 Digit Numbers – Partitioning by Place Value”. Part 2 focuses on building and solving 2 Digit Addition questions that require regrouping. You will then compare this method to the traditional algorithm.
You will need access to one of the following:
- Physical Base Ten Blocks (tens and ones)
- Printable Base Ten blocks (print in black and white OR color)
- Virtual Base Ten Blocks e.g. CPM Tiles
The correct name for this strategy is decomposing because you are partitioning by place value.
Formative Assessment
Number Sentences – 2 questions with 3 parts each. For each question, students determine if each of the 3 number sentences shows a way to represent the word problem and provide an explanation. Student exemplars included. <Original Website>




