Conservation of Number and Equality
Conservation of Number:
Definition:
Quantity does not change regardless of the physical arrangement. For example, no matter how you rearrange the number 24, you still have a value of 24: 12 + 12, 20 + 4, 21 + 3, 10 + 10 + 4
When is this property introduced?
The foundations for conservation of number are introduced when students begin counting objects using one to one correspondence.
Students will struggle with regrouping when representing numbers (ie. 24: 24 ones regrouped to 1 ten and 14 ones regrouped to 2 tens and 4 ones) if they are not building those representations on the understanding of conservation of number. If students do not recognize that regrouping doesn’t change the value of the number, how will they add or subtract? Multiply and divide?
How might this property be introduced?
Many models can be utilized to represent conservation of number. Below, you will find conservation of number explored from Kindergarten to Grade 9.
The “Concept Attainment” Strategy
“Equality – Developing the Concept” includes a slideshow that can be used to explore the concept of Equality using the “Concept Attainment Strategy”. You can read more about the “Concept Attainment Strategy” here.
Exploring Conservation of Number throughout the grades:
The processes for implementing conservation of number are scripted. This is NOT to script you but to provide you with a possible process for implementation. Please adapt to your style and the needs of your students!
Kindergarten
CURRENT Curricular Outcomes:
Represent and describe numbers 2 to 10, concretely and pictorially.
Process of Complexity:
Spend a lot of time focusing on sums to 5. Once students demonstrate understanding, move to sums of up to 10.
Key Vocabulary:
The following key vocabulary should be used with and by students. Words in italics are not expected at this grade level. They are included here as a support for the teacher. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- Quantity
- How many
- Represent
- Number
- Demonstrate
- Build (Compose)
- Break apart (Decompose)
The Process:
Note: Students will work with concrete manipulatives. Stick with 5 objects for the activities listed below for a period of time to really build an understanding of 5. Each time you do the activity, you can switch out the objects for new objects. As students are ready, move on to 6, 7, etc.
Strategy Part 1: Concrete
> How many do you see?
- Place 5 objects (ex. blocks) on display so that all students can easily see them.
- Have students place a fist in front of their chest. Ask, “Look at the blocks. In your head, answer the question – how many do you see? When you know, put a thumb up.” Wait until most or all have thumbs up.
- “Turn to your partner. How many blocks did you see? How did you figure that out?”
- Discuss as a class. Make sure that, in the end, they all agree that there are 5 blocks.
> Move them around without adding or removing any.
- “Now, watch carefully! I’m going to move these around.” Move the blocks around slowly. Do not try to trick them. They need to see that none were added or removed.
- Using fist in front of chest again, “Think to yourself – how many are there? What quantity of blocks do you see?”
- Students can discuss with a partner. Class share. Recount if needed.
- “Why aren’t there more blocks?” Because none were added.
- “Why aren’t there less blocks?” Because none were removed.
- “So the number of blocks, the quantity of blocks, didn’t change.”
Strategy Part 2: Concrete
> Spread them out.
- “I’m going to move these around again.” Spread them far out.
- I want you to think “are there more? The same amount? Less? Close your eyes. Picture the objects. When you are ready, if you think there are more, give me a thumbs up. If you think there are less, give me a thumbs down. If you think it is the same amount, put your thumb sideways.”
- Use this as a formative assessment to check on which students understand / don’t understand conservation of number.
- “Put your thumbs away. Open your eyes. Discuss with your partner.” Class discussion.
> Squish them close.
- Repeat this question after squishing the objects close together.
- “What number of blocks do we have? How many are there now”
- “This time, I want you to picture moving the objects in your head. How many are there now?”
Strategy Part 3: Concrete
> Students break apart (decompose) into smaller groups.
- Give each student 5 objects.
- “This time, we are going to represent our thinking on the board. First we built a pile of 5.”
- On the board, write the header: Built
- Have them count the blocks.
- “How many blocks are there?” 5
- Write 5 under the header Built.
- “We are going to break apart this big pile into 2 piles. You might give them the Concrete Mat to work on and use the Google Slides version (for displaying)
- On the board, write the header: “First Pile” beside “Built”
- Ask a student how many they put in the first pile. Ex. They may say a pile of 2.
- Write “2” below the header First Pile. Write “Second Pile” beside “First Pile”
- Ask that same student how many they put in the second pile. Ex. They say 3.
- Write “3” below “Second Pile.”
- “You started with a pile of 5. You broke that pile apart into a pile of 2 and a pile of 3.”
- Ask, “Who else placed 2 in the first pile and 3 in the second pile?”
> Repeat for all other possible “break aparts”
- Ask, “Who broke apart their piles in a different way?”
- Ask, “How many did you start with?” 5
- Write this number under “built”.
- Ask, “How many did you place in the first pile?” ex. 4
- Write this number under “First pile”
- Ask, “How many did you place in the second pile?” ex. 1
- Write this number under “Second pile.”
- Repeat until you have all the different variations. (1, 4) (2, 3) (3, 2) (4, 1) and maybe even (0,5) and (5,0)
> Look for Patterns
- Ask students to look at the numbers on the board. Ask, “What do you notice? Give me a thumbs up when you one thing. Don’t stop. Keep looking. When you notice something else, put up another finger.”
- Ask students to share what they noticed.
- They may identify any of the following patterns:
- “Built” always has 5’s.
- The numbers 0-5 show up exactly once in each Pile column.
- Looking at a single row: Pile 1 and Pile 2 always equal 5.
Formative / Summative Assessment:
Show # of objects. “How many are there?”
Move them around. “How many are there?” “How do you know?”
Listen for evidence that the student understands that the quantity doesn’t change if you don’t add any or remove any objects.
Moving Forward:
Once students are comfortable with 5, work with 5 dots, 5 on a rekenrek, etc.
Then, move on to other numbers up to 10 and repeat.
Grade 1
CURRENT Curricular Outcomes:
Represent and describe numbers to 20, concretely, pictorially and symbolically.
Demonstrate an understanding of addition of numbers with answers to 20 and their corresponding subtraction facts, concretely, pictorially and symbolically.
Process of Complexity:
Spend a lot of time focusing on sums to 5. Once students demonstrate understanding, move to sums of up to 10. Once students demonstrate understanding, move to sums within 20.
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- Equality
- Relationship
- Quantity
- Addition
- Subtraction
- Operations
- Compose
- Decompose
- Part-part-whole
- Patterns
Pre-Assessment:
> Complete Kindergarten strategy part 1 as a class.
- Identify which students know, without counting, that moving the objects doesn’t change the count.
- You may need to repeat Kindergarten strategies parts 1 and 2 with individual students to identify specifically where they are struggling.
The Process:
Strategy Part 1: Concrete
> Students decompose the whole into smaller parts.
- Provide each student with 5 objects (ex. blocks) and the Concrete – Composing and Decomposing Student Mats.
- The Google Slides version can be used for projecting.
- Tell students to “Place all of the blocks into the “whole” section on the mat. These blocks will represent our whole set of blocks for this activity.”
- Students place the 5 blocks in the “whole” section on the mat.
- Tell students to “Move some of the blocks from the “whole” into in the first “Parts” section and the rest in the second “Parts” section.”
- Ask a student (Ex. Johnny) “How many blocks did you have altogether?”
- When he says he has 5, write 5 in the “Record” section.
- Ask “who else has 5 blocks?” Everyone’s hand should raise.
- Point at the 5 and say “Johnny saw a quantity of 5”
- Write “=” and say “which is the same number of blocks as”
- Write “5” and say “the 5 blocks everyone else saw”.
> Introduce the Equals Sign and the concept of Relationship
- Ask, “Who knows what this symbol (point to the equals sign) is?”
- If nobody states that it is the equal sign, tell them “We call this an equal sign.”
- Say, “An equal sign is used to show a relationship. Who can tell me what the relationship is between the left side of the equal sign and the right side of the equal sign?” Johnny saw 5 blocks which is the same number of blocks as what everyone else saw.
- Ask another student, “How did you split the blocks?” The student says, “I split them into 4 and 1”.
- Say “You have 5 blocks.” Write 5
- Say “And you broke them” Write =
- Say “into 4 and 1”. Write 4 + 1
- Ask, “Did the total number of blocks change? Do we still have the same quantity we began with?” Yes.
- Ask another student how they many blocks they have. Linda says, “5”. Write 5.
- Ask, “How did you break the blocks into 2 groups? How did you decompose the 5 blocks?” (You can show hands together when you say 5 and move your hands apart to show decomposition)
- “I have 2 and 3”.
- Say “You took your 5 blocks” Point to the 5.
- Say “and you decomposed those 5 blocks into” Write =
- Say “a part with 2 and a part with 3”. Write 2 + 3.
- Ask, “Does Linda still have 5 blocks altogether?” Yes.
- Say, “The first student decomposed his blocks into parts of 4 and 1 and Linda decomposed hers into 2 and 3. 4 plus 1 (write 4 + 1) is the same number of blocks as (write =) 2 plus 3 (write 2 + 3)”
- Ask, “What is the relationship between how the the first student decomposed their 5 blocks and how Linda decomposed her 5 blocks?” They both equal 5.
- Repeat for a few other students, always writing new equations below previous equations.
> Using what you know to determine unknown value in an equation
- Obtain the information from a student and write it down for the left side: ex. 3 + 2 =
- Say, “I decomposed my 5 blocks. I’m not going to tell you how many is in my first part.” Write a ___
- Say, “but my second part has 3 blocks”. Write + 3
- Ask, “How many blocks are in my first part?” Point to the line.
- Give students some time to think individually.
- Ask them to explain to a partner how they figured out what should be written on the line.
- Have a class discussion.
- When the class comes to consensus, write 2 on the line.
Strategy Part 2: Pictorial
> Use Dots rather than blocks
- Repeat the process from Strategy Part 1 but show dot arrangements and ask the question “how do you see the dots?” (Google Docs, PDF, Google Slides)
- You can cover up a portion of the dots to represent the unknown.
Strategy Part 3: Symbolic
> Rearrange parts into new parts
- Give students 5 objects.
- Write 1 + 4 on the board.
- Say “arrange your blocks so that you can clearly see 1 + 4.”
- Write = 2 + __ so that you now have 1 + 4 = 2 + __
- Say “move enough blocks from one pile to the other pile so that you now show 2 +___”
> Record the rearrangement of parts using arrows
- Have students explain to their partner how many blocks they moved. Have a student share how many they moved.
- When the student says they moved one block from the 4 to the 1, draw the arrow and number of blocks being moved.
- Say “So now there isn’t 1 block in that pile. How many are there?” 2
- Say, “So the the 1 became 2. What did the 4 become?” 3
- Ask, “Why?” because 3 is one less than 4 OR when you remove one from 4 you end up with 3.
- Practice with a few more simple examples like the one above. Students build, class discusses, teacher records representations on the board. Ex:
- 2 + 6 = 3 + __
- 5 + 2 = __ + 4
- 3 + __ = 4 + 6
- __ + 1 = 6 + 2
- 4 + __ = 5 + __
- After students are comfortable, tell students to picture the next one in their head but don’t build it yet. 5 + 7 = 3 + __ Can they figure out what goes on the blank? Have them show their visualizing using the example above as a guideline on their mini whiteboard, build to check and explain to a partner.
- Repeat with other examples…first visualizing to figure out the answer, responding on their whiteboards, building to check and explaining to a partner.
- As students become more confident, they won’t have to build to check but should still complete the rest.
Formative / Summative assessment:
Make the following statement true: 5 + 9 = __ + 8 Convince me.
Moving Forward:
Once students are comfortable with 5, work with 5 dots, 5 on a rekenrek, etc.
Then, move on to other numbers up to 10 and repeat.


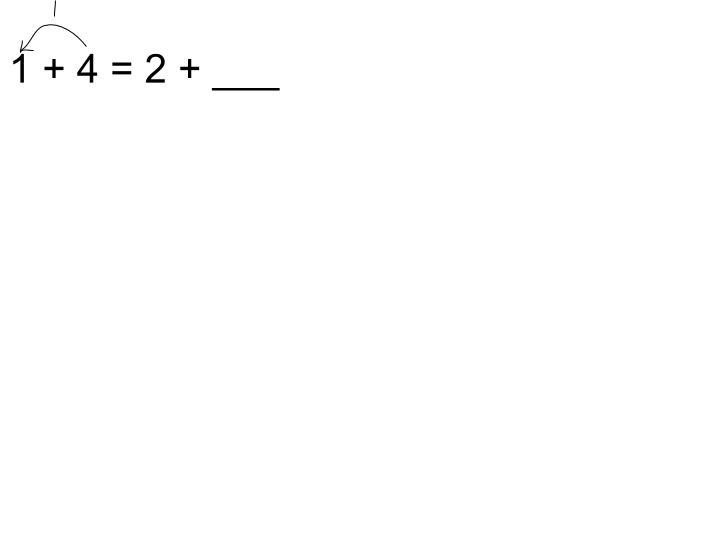
Grade 2
CURRENT Curricular Outcomes:
Represent and describe numbers to 100, concretely, pictorially and symbolically.
Demonstrate an understanding of addition (limited to 1-and 2-digit numerals) with answers to 100 and the corresponding subtraction.
Apply mental mathematics strategies for basic addition facts and related subtraction facts to 18.
Process of complexity:
Spend a lot of time focusing on number facts to sums up to 10. Once students demonstrate understanding, move to single digit numbers with sums within 18. Once students demonstrate understanding, move to sums within 100.
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- Quantity
- Equal
- Equal sign
- Not equal
- Not equal sign
- Addition
- Subtraction
- Operations
- Additive thinking strategies
- Patterns
- Relationship
Pre-Assessment:
> Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student who do not answer MIPI+ Question #1 correctly:
- Complete Kindergarten Strategy Part 1 as a class using between 6-10 objects
- Identify which students know without counting that moving the objects doesn’t change the count.
- You may need to repeat Kindergarten and Grade 1 strategies with individual students to identify specifically where they are struggling.
The Process:
Strategy Part 1: Concrete
This process begins with an image, however, it will lead into concrete.
> Quick Image
- Tell students you will be quickly flashing an image with dots on the screen. They need to figure out how many dots there are altogether. As they are thinking, they will hold a fist in front of their chest. When they think they know the answer, they put up a thumb. (Google Slides)
- Ask the question: How many dots do you see? Display the image on the right for 3 seconds. (Slide 2-3)
- Tell them you will show it again so they can check. Flash it again for 3 seconds.
- Repeat until everyone has their thumbs up.
- Display the image again.
- Have students to show and tell their partner how they figured out how many dots there were.
- Have students share as a class. A variety of strategies will be shared.
- Explain that you will be exploring a specific strategy that will be helpful when they are solving addition questions. It is a powerful additive thinking strategy.” (hopefully shared by a student)
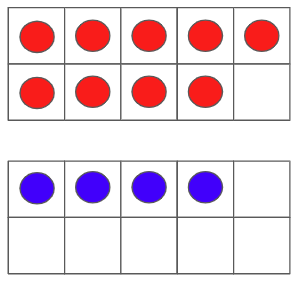
> Decomposing and Recomposing
- Here’s a totally made up story that might be helpful.
- Mathematicians like everything nice and tidy when they are done (even though doing math can be very messy). When they see two ten frames together like this, they love to take from one in order to fill up the other. (If you can, show this movement so you get the image on the right…or have it ready on another screen.
- Say, “We started with this image” (Slide 6)
- Have students rebuild it on their ten frame.
- Ask, “How would we write this as an addition statement?” 9 + 4 Write this on the board below the first image. (Slide 6 after 1 click)
- Say “We took from one to fill up the other one.” Have them do this. (Slide 7)
- Ask, “What did addition statement we end up with?” 10 + 3 Write this on the board below the second image. (Slide 7 after 1 click)
- Ask “Is 9 plus 4 is the same total number of dots as 10 plus 3? Do we still have the same total quantity?” Let them figure it out.
- Discuss.
- Say “Yes, 9 plus 4 is the same total number of dots as 10 plus 3. We can show that by writing an equals sign in between the two statements.” Write the equals sign between them. (Slide 7 after another click)
- Let’s practice with another one. Display a ten frame of 3 + 9. Have students build it and write down the original statement (3 + 9)
- Have them move the blocks. Share as a class.
- Ask students what the new statement is and write it down on the board. (2 + 10) Have students also write it down.
- Ask, “How do I show that 3 + 9 is the same number of dots as 2 + 10?” Write an equals sign. Have students do this with you.
- Ask, “What relationship does the equal sign show in this equation?”
- To increase complexity, repeat for other questions such as
- 8 + 3 (8 instead of 9)
- 4 + 8 (8 is second)
- Stick to numbers up to 9.
Strategy Part 2: Pictorial
Repeat process as above
- Instead have them visualize the dots rather than building the dots.
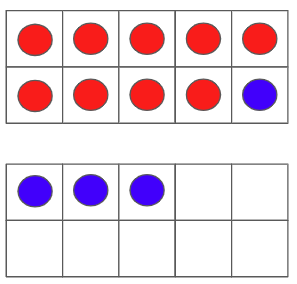
Strategy Part 3: Symbolic
Explore equations without blocks to create their equality equations.
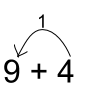
- Write 9 + 4 on the board.
- Say “imagine the ten frames that represent 9 + 4”.
- Ask, “What would you do? What quantity would you move over?” move one from the 4 to fill up the 9.
- Draw an arrow from the four to point to the nine. Draw 1 above the arrow to show that one block is moving.
- Ask, “What is the new statement?” 10 + 4
- Ask, “How do I show that 9 + 4 is the same number of blocks as 10 + 4?” Equals sign
- Write the equal sign.
- Have students try some of the following questions.
|
|
Connect to Multiplication
- Write 2 x 4 = __ x 2 on the board
- Say, “How might what we have learned help you figure out what to write on this line to make this statement true?”
- Give students time to work.
- Use other examples that explore the commutative property.
Formative / Summative assessment:
-
Make the following statement true: 54 + 29 = __ + 30 Convince me.
Grade 3
CURRENT Curricular Outcomes:
Represent and describe numbers to 1000, concretely, pictorially and symbolically.
Describe and apply mental mathematics strategies for adding two 2-digit numerals.
Demonstrate an understanding of addition and subtraction of numbers with answers to 1000 (limited to 1-, 2- and 3-digit numerals), concretely, pictorially and symbolically.
Process of complexity:
Start with two-digit plus two-digit addition questions. When students demonstrate understanding, move to three digit numbers where the solution does not exceed 1000.
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- Additive Thinking Strategies
- Compose
- Decompose
- Equation
- Expressions
- Symbols
- Values
- Unknown Values
- One-step equation
- Relationship
Pre-Assessment:
> Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student(s) who do not answer MIPI+ Question #1 correctly:
- Complete Kindergarten Strategy Part 1 as a class using between 6-10 objects
- Identify which students know without counting that moving the objects doesn’t change the count.
- You may need to repeat previous strategies with individual students to identify specifically where they are struggling.
The Process:
Strategy Part 1: Concrete
> Decomposing and Recomposing
- Provide each student with
- Base 10 blocks that equal 100: Eight 10 blocks and twenty 1 blocks
- Concrete – Composing and Decomposing Student Mats.
- The Google Slides version can be used for projecting
- Tell students to “Place all of the blocks into the “whole” section on the mat. These blocks will represent our whole set of blocks for this activity.”
- Students place the base 10 blocks equaling 100 in the “whole” section on the mat.
- Tell students to “Move some of the blocks from the “whole” into in the first “Parts” section and the rest in the second “Parts” section.”
- Ask a student (Ex. Johnny) “What is the value of the base 10 blocks you have altogether?”
- When he says he has 100, write 100 in the “Record” section.
- Ask “who else has a value of 100?” Everyone’s hand should raise.
- Point at the 100 and say “Johnny saw a value of 100”
- Write “=” and say “which is the same value as”
- Write “100” and say “the 100 everyone else saw”.
> Review the Equals Sign and the concept of Relationship
- Ask, “Who knows what the purpose of this symbol (point to the equals sign) is?” Class discussion.
- Say, “An equal sign is used to show a relationship. Who can tell me what the relationship is between the left side of the equal sign and the right side of the equal sign?” Johnny has a value of 100 which is the same value as what everyone else has.
- Ask another student, “How did you split the blocks? What is the total value you have in each part?” The student says, “I split them into “25” and “75”.
- Say “You have a total value of 100.” Write 100
- Say “And you broke them” Write =
- Say “into values of 25 and 75. We express this as…”. Write 25 + 75.
- Ask, “Did the total value of the blocks change? Do we still have the same value we began with?” Yes.
- Ask another student the total value of her blocks. Linda says, “100”. Write 100.
- Ask, “ How did you decompose the blocks?” (You can show hands together when you say 100 and move your hands apart to show decomposition)
- “I have 80 and 20”.
- Say “You took your blocks with a value of 100” Point to the 100.
- Say “which you expressed as” Write =
- Say “80 and 20”. Write 80 + 20.
- Ask, “Does Linda still have a total value of 100?” Yes.
- Say, “The first student decomposed his blocks into parts of 25 and 75 and Linda decomposed hers into 80 and 20. 25 plus 75 (write 25 + 75) is the same value as (write =) 80 plus 20 (write 80 + 20)”
- Say, “The expression 25 plus 75 is the same value as the expression 80 plus 20.”
- Ask, “What is the relationship between how the the first student decomposed their blocks and how Linda decomposed her blocks?” They both equal 100.
- Repeat for a few other students, always writing new equations below previous equations.
> Using what you know to determine unknown value in an equation
- Obtain the information from a student and write it down for the left side: ex. 83 + 17 =
- Say, “I decomposed my 100. I’m not going to tell you how many is in my first part.” Write a ___
- Say, “but my second part has a value of 16”. Write + 16
- Ask, “What is the value of my first part?” Point to the line.
- Give students some time to think individually.
- Ask them to explain to a partner how they figured out what should be written on the line.
- Have a class discussion.
- When the class comes to consensus, write 84 on the line.
- Ask, “Did anyone solve it without figuring out what 100 – 16 is?”
- Students should be able to explain that they moved one from the 17 over to the 83 to end up with 16 and 84.
Strategy Part 2: Pictorial
Repeat process as above
- Instead have them draw or visualize the base ten blocks and the movement that is involved.
Strategy Part 3: Symbolic
Explore equations without blocks to create their equality equations.
- Provide each student with Base 10 blocks. Ten 10 blocks and twenty 1 blocks.
- Write 26 + 18 on the board.
- Say “arrange your blocks so you can clearly see 26 + 18.”
- Write = __ + 20 on the board so that you now have 26 + 18 = __ + 20
- Say “move enough blocks from one pile to the other pile so that you now show something plus 20.”
- Have students explain to their partner how many blocks they moved. Have a student share how many they moved.
- When the student says they moved 2 blocks from the 26 to make the 18 into 20, draw the arrow and numbeof blocks being moved.
- Ask, “Why would we move 2 blocks from the 26 to the 18?” To make 20 so it matches.
- Say, “So now there isn’t 26 blocks in the first part. How many are there?” 24. Write 24 on the line.
- Ask, “What’s the benefit to moving the blocks to make 24 plus 20?” Because it’s easier to add 24 and 20 versus 26 and 18.
- Practice with a few more examples, writing them on the board. Students should be moving to pure symbolic as they are ready: building and then representing symbolically on mini whiteboards ==> writing symbolically and building to check ==> writing symbolically.
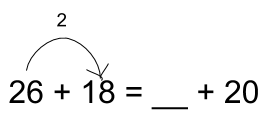
|
|
Formative / Summative assessment:
-
Make the following statement true: 254 + 329 = __ + 330 Convince me.
Grade 4
CURRENT Curricular Outcomes:
Demonstrate an understanding of addition of numbers with answers to 10 000 and their corresponding subtractions (limited to 3- and 4-digit numerals).
Represent and describe decimals (tenths and hundredths), concretely, pictorially and symbolically.
Demonstrate an understanding of addition and subtraction of decimals (limited to hundredths).
Process of complexity:
Start by focusing on additive thinking strategies that can be applied to whole numbers within 100. This will allow students to explore a strategy, if they have not seen it before, using less complex numbers. Once students demonstrate understanding, move to whole numbers within 1000. Once students demonstrate understanding, move to whole numbers within 10 000. Once students demonstrate understanding of additive thinking strategies for whole numbers, move to decimals using dollars.
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- Equal
- Equal sign
- Whole numbers
- Decimals
- Mental math
- Addition
- Subtraction
- Operations
- Additive Thinking Strategies
- Equation
- Expression
- Algorithm
- Patterns
Pre-Assessment:
> Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student(s) who do not answer MIPI+ Question #1 correctly:
- Complete Kindergarten Strategy Part 1 as a class using between 6-10 objects
- Identify which students know without counting that moving the objects doesn’t change the count.
- You may need to repeat Kindergarten and Grade 1 strategies with individual students to identify specifically where they are struggling.
The Process:
Strategy Part 1: Concrete
> Decomposing and Recomposing
- Provide each student with
- Base 10 blocks that equal 100: Eight 10 blocks and twenty 1 blocks
- Concrete – Composing and Decomposing Student Mats.
- The Google Slides version can be used for projecting
- Tell students to “Place all of the blocks into the “whole” section on the mat. These blocks will represent our whole set of blocks for this activity.”
- Students place the base 10 blocks equaling 100 in the “whole” section on the mat.
- Tell students to “Move some of the blocks from the “whole” into in the first “Parts” section and the rest in the second “Parts” section.”
- Ask a student (Ex. Johnny) “What is the value of the base 10 blocks you have altogether?”
- When he says he has 100, write 100 in the “Record” section.
- Ask “who else has a value of 100?” Everyone’s hand should raise.
- Point at the 100 and say “Johnny saw a value of 100”
- Write “=” and say “which is the same value as”
- Write “100” and say “the 100 everyone else saw”.
> Review the Equals Sign and the concept of Relationship
- Ask, “Who knows what the purpose of this symbol (point to the equals sign) is?” Class discussion.
- Say, “An equal sign is used to show a relationship. Who can tell me what the relationship is between the left side of the equal sign and the right side of the equal sign?” Johnny has a value of 100 which is the same value as what everyone else has.
- Ask another student, “How did you split the blocks? What is the total value you have in each part?” The student says, “I split them into “25” and “75”.
- Say “You have a total value of 100.” Write 100
- Say “And you broke them” Write =
- Say “into values of 25 and 75. We express this as…”. Write 25 + 75.
- Ask, “Did the total value of the blocks change? Do we still have the same value we began with?” Yes.
- Ask another student the total value of her blocks. Linda says, “100”. Write 100.
- Ask, “ How did you decompose the blocks?” (You can show hands together when you say 100 and move your hands apart to show decomposition)
- “I have 80 and 20”.
- Say “You took your blocks with a value of 100” Point to the 100.
- Say “which you expressed as” Write =
- Say “80 and 20”. Write 80 + 20.
- Ask, “Does Linda still have a total value of 100?” Yes.
- Say, “The first student decomposed his blocks into parts of 25 and 75 and Linda decomposed hers into 80 and 20. 25 plus 75 (write 25 + 75) is the same value as (write =) 80 plus 20 (write 80 + 20)”
- Say, “The expression 25 plus 75 is the same value as the expression 80 plus 20.”
- Ask, “What is the relationship between how the the first student decomposed their blocks and how Linda decomposed her blocks?” They both equal 100.
- Repeat for a few other students, always writing new equations below previous equations.
> Using what you know to determine unknown value in an equation
- Obtain the information from a student and write it down for the left side: ex. 83 + 17 =
- Say, “I decomposed my 100. I’m not going to tell you how many is in my first part.” Write a ___
- Say, “but my second part has a value of 16”. Write + 16
- Ask, “What is the value of my first part?” Point to the line.
- Give students some time to think individually.
- Ask them to explain to a partner how they figured out what should be written on the line.
- Have a class discussion.
- When the class comes to consensus, write 84 on the line.
- Ask, “Did anyone solve it without figuring out what 100 – 16 is?”
- Students should be able to explain that they moved one from the 17 over to the 83 to end up with 16 and 84.
Strategy Part 2: Pictorial
Repeat process as above
- Instead have them draw or visualize the base ten blocks and the movement that is involved.
Strategy Part 3: Symbolic
Explore equations without blocks to create their equality equations.
- Provide each student with Base 10 blocks. Ten 10 blocks and twenty 1 blocks.
- Write 34 + 57 on the board.
- Say “arrange your blocks so you can clearly see 34 + 57.”
- Write = __ + 60 on the board so that you now have 34 + 57 = __ + 60
- Say “move enough blocks from one pile to the other pile so that you now show something plus 60.”
- Have students explain to their partner how many blocks they moved. Have a student share how many they moved.
- When the student says they moved 3 blocks from the 34 to make the 57 into 60, draw the arrow and number of blocks being moved.
- Ask, “Why would we move 3 blocks from the thirty four to the fifty-seven?” To make 60 so it matches.
- Say, “So now there isn’t 34 blocks in the first part. How many are there?” 31. Write 31 on the line.
- Ask, “What’s the benefit to moving the blocks to make 31 plus 60?” Because it’s easier to add 31 and 60 versus 34 and 57.
- Practice with a few more examples, writing them on the board. Students should be moving to pure symbolic as they are ready: building and then representing symbolically on mini whiteboards ==> writing symbolically and building to check ==> writing symbolically.
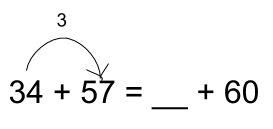
|
|
> Making Connections to Decimals
- Use Base Ten Blocks to introduce students to decimals. The 100 is now 1, 10 is now 0.1, 1 is now 0.01. You might find this video helpful when renaming the Base Ten Blocks for use with decimals. Instead, you may choose to make the 1000 worth 1. NOTE: Draft curriculum is limited to tenths. Current curriculum includes hundredths. Repeat the process above using decimals.
- You can use ten frames for decimals as well. Review the quick images process used in Grade 2 with ten frames. Change the value of one ten frame to 1. This means that 9 dots in the ten frame is valued at 0.9 rather than 9.
Connect to Multiplication
- Write 2 x 4 = __ x 8 on the board
- Say, “How might what we have learned help you figure out what to write on this line to make this statement true?”
- Give students time to work.
- Use other examples that explore the doubling / halving strategy.
Formative / Summative assessment:
-
Make the following statement true: 254 + 329 = __ + 330 Convince me.
Grade 5
CURRENT Curricular Outcomes:
Demonstrate an understanding of addition and subtraction of decimals (limited to thousandths).
Process of complexity:
Start by focusing on additive thinking strategies that can be applied to decimal numbers limited to tenths. This will allow students to explore a strategy, if they have not seen it before, using less complex numbers. Once students demonstrate understanding, move to hundredths. Once students demonstrate understanding, move to thousandths.
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- Equation
- Variable
- Single-variable
- Unknown
- One-step equations
- Solutions
- Patterns
Pre-Assessment:
> Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student(s) who do not answer MIPI+ Question #1 correctly:
- Complete Kindergarten Strategy Part 1 as a class using between 6-10 objects
- Identify which students know without counting that moving the objects doesn’t change the count.
- You may need to repeat Kindergarten and Grade 1 strategies with individual students to identify specifically where they are struggling.
The Process:
Strategy Part 1: Concrete
> Rename Base 10 Blocks to decimals
- Use Base Ten Blocks to introduce students to decimals. The 1000 is now 1, 100 is now 0.1, 10 is now 0.01, 1 is now 0.001. You might find this video helpful when renaming the Base Ten Blocks for use with decimals though you will notice that it makes the 100 worth 1.
> Decomposing and Recomposing
- Provide each student with
- Base ten blocks that equal 1: eight 0.1 blocks and twenty 0.01 blocks
- Concrete – Composing and Decomposing Student Mats.
- The Google Slides version can be used for projecting
- Tell students to “Place all of the blocks into the “whole” section on the mat. These blocks will represent our whole set of blocks for this activity.”
- Students place the base 10 blocks equaling 1in the “whole” section on the mat.
- Tell students to “Move some of the blocks from the “whole” into in the first “Parts” section and the rest in the second “Parts” section.”
- Ask a student (Ex. Johnny) “What is the value of the base 10 blocks you have altogether?”
- When he says he has 1, write 1 in the “Record” section.
- Ask “who else has a value of 1?” Everyone’s hand should raise.
- Point at the 1 and say “Johnny saw a value of 1”
- Write “=” and say “which is the same value as”
- Write “1” and say “the 1 everyone else saw”.
> Introduce the Equals Sign and the concept of Relationship
- Ask, “Who knows what the purpose of this symbol (point to the equals sign) is?” Class discussion.
- Say, “An equal sign is used to show a relationship. Who can tell me what the relationship is between the left side of the equal sign and the right side of the equal sign?” Johnny has a value of 1 which is the same value as what everyone else has.
- Ask another student, “How did you split the blocks? What is the total value you have in each part?” The student says, “I split them into “0.3” and “0.7”.
- Say “You have a total value of 1.” Write 1
- Say “And you broke them” Write =
- Say “into values of 3 tenths and 7 tenths. We express this as…”. Write 0.3 + 0.7.
- Ask, “Did the total value of the blocks change when you decomposed the 1 into two parts? Do we still have the same value we began with?” Yes.
- Ask another student the total value of her blocks. Linda says, “1”. Write 1.
- Ask, “ How did you decompose the blocks?” (You can show hands together when you say 100 and move your hands apart to show decomposition)
- “I have 8 tenths and 2 tenths”.
- Say “You took your blocks with a value of 1” Point to the 1.
- Say “which you expressed as” Write =
- Say “8 tenths and 2 tenths”. Write 0.8 + 0.2.
- Ask, “Does Linda still have a total value of 100?” Yes.
- Say, “The first student decomposed his blocks into parts of 3 tenths and 7 tenths and Linda decomposed hers into 8 tenths and 2 tenths. 3 tenths plus 7 tenths (write 0.3 + 0.7) is the same value as (write =) 8 tenths plus 2 tenths (write 0.8 + 0.2)”
- Say, “The expression 3 tenths plus 7 tenths is the same value as the expression 8 tenths plus 2 tenths.”
- Ask, “What is the relationship between how the the first student decomposed their blocks and how Linda decomposed her blocks?” They both equal 1.
- Repeat for a few other students, always writing new equations below previous equations.
Strategy Part 2: Pictorial
Repeat process as above
- Instead have them draw or visualize the base ten blocks and the movement that is involved.
Strategy Part 3: Symbolic
Explore equations without blocks to create their equality equations.
- Provide each student with Base 10 blocks. Approximately ten 0.1 blocks and twenty 0.01 blocks.
- Write 0.43 + 0.38 on the board.
- Say “arrange your blocks so you can clearly see forty-three hundredths + thirty-eight hundredths.”
- Write = __ + 0.40 on the board so that you now have 0.43 + 0.38 = __ + 0.40
- Say “move enough blocks from one pile to the other pile so that you now show something plus 4 tenths.”
- Have students explain to their partner how many blocks they moved. Have a student share how many they moved.
- When the student says they moved 2 blocks (0.02) from the 0.43 to make the 0.38 into 0.4, draw the arrow and number of blocks being moved.
- Ask, “Why would we move two hundredths from the forty-three hundredths to the thirty-eight hundredths?” To make four tenths (or forty hundredths) so it matches.
- Say, “So now there isn’t forty-three hundredths in the first part. How many are there?” forty-one hundredths. Write 0.41 on the line.
- Ask, “What’s the benefit to moving the blocks to make forty-one hundredths plus forty-hundredths (or four tenths)?” Because it’s easier to add 0.41 and 0.4 versus 0.43 and 0.38.
- Practice with a few more examples, writing them on the board. Students should be moving to pure symbolic as they are ready: building and then representing symbolically on mini whiteboards ==> writing symbolically and building to check ==> writing symbolically.
- Have students create their own questions showing the original expression and a new expresion after making a move that makes sense.
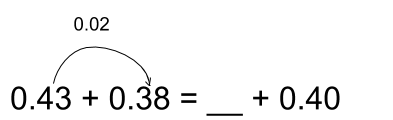
Grade 6
CURRENT Curricular Outcomes:
Solve problems involving whole numbers and decimal numbers.
Demonstrate and explain the meaning of preservation of equality, concretely and pictorially.
Process of complexity:
Start by focusing on whole numbers less than 10. When students demonstrate understanding, move to larger numbers.
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- Equation
- Variable
- Unknown
- Solutions
- Patterns
Pre-Assessment:
> Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student(s) who do not answer MIPI+ Question #1 correctly:
- Complete Kindergarten Strategy Part 1 as a class using between 6-10 objects
- Identify which students know without counting that moving the objects doesn’t change the count.
- You may need to repeat previous strategies with individual students to identify specifically where they are struggling.
Mini “App”
We have also created a simple mini “app” that students can access online to introduce this concept.
The Process:
Strategy Part 1: Concrete and Part 2: Pictorial (together)
> “Bears in a Bag” Introduction
- Provide each pair of students with a paper bag, approximately 30 unifix cubes, 1 balance scale, and 2 copies of the handout. Have an extra paper bag per group ready to go.
- Project the slide show “Bears in a Bag”
- Slide 2:
- Say, “You have a special balance scale. It only stays in balance if the quantity of bears on each side is the same.”
- Slide 3:
- Say, “There are 4 bears on the left side. How many bears do I need to balance this?” 4
- Slide 4:
- Say, “If I put 4 bears in the bag,”
- Draw 4 bears
- Write 4 in the table under bag.
- Ask, “how many bears do you need to put on the other side to balance it?” 4
- Write 4 in the second column.
- Ask, “What if I added one more bear to the bag?” Draw 1 more bear.
- Ask, “What would I need to do?” Add 1 more bear to the other side.
- Write 5 and 5 in the table.
- Repeat for numbers 7 and 1 million.
- Say, “I put 3 bears in the bag and 2 to balance it.” Students should complain.
- Slide 5:
- Say, “There are six bears balanced with a bag of bears. Take a moment to think to yourself. How many bears are in the bag?” 6
- Slide 6:
- Say, “Without letting your partner see, place some bears inside your bag. Place it on one side of the scale. Place the quantity of bears needed to balance this on the other side of the scale. Partner 2, you need to figure out how many bears are in the bag without peaking. Empty the bag to check. Switch roles once.”
- Give 2 minutes for students to practice. This is to help them understand the process.
- Slide 7:
- Say, “Take out your handout. The question on the screen is the same as the first question in your handout. Four bears is the same amount of bears as one bag of bears. Let’s draw a picture.”
- Draw the bag. Draw the bears. Don’t get fancy! Have students do this as well.
- Ask, “How many bears are in the bag?” 4
- Say, “There are 4 bears in the bag.”
- Write 4 on the blank.
- Slide 8:
- Say, “Now it’s your turn to create a problem. In the second column, write a problem similar to the one we just did. Maybe it’s the one you built for your partner. Write out the full sentences! Draw a picture to match. Fill in the answer.”
- Give students some time to do this.
- Slide 9:
- Say, “This time, we have a bag of bears and one on the outside. How many bears would I need to place on the left side so that it balances if there are 5 bears in the bag?”
- Write 5 under bag.
- When students respond 6, write 6 under all.
- Ask, “How is this affected if I add one more bear to the bag?” Need to add another bear to the other side.
- Ask, “How is this affected if I remove 3 bears from the bag?” Need to remove 3 bears from the other side.
- Ask, “I want to change the quantity of bears on each side but keep everything in balance. What could I do?” Students should talk about adding or removing the same # from both sides. Record this changes and place in table.
- Slide 10:
- Say, “Four bears is the same number of bears as one bag of bears and one bear on the outside. Take a moment to figure out how many bears are in the bag.” 3
- Ask, “How did you figure that out?”
- Slide 11:
- Students repeat this process building for each other. They do this twice each.
- Slide 12:
- Read the question.
- Draw the visual with students.
- Students figure it out and share answers.
- Slide 13:
- Students create their own versions, draw the visual and solve.
- Slide 14:
- Say, “There is a special rule about bags. If I use more than one bag, all of the bags must have the exact same number of bears in each of them.”
- Slide 15:
- Say, “If I put 2 bears in the first bag, there must be 2 bears in the second bag. If I put 3 bears in the first bag, there must be 3 bears in the second bag.”
- Ask, “If I put 20 bears in the first bag, how many are in the second bag?” 20.
- Say, “So I put 4 bears in the first bag and 3 bears in the second bag…” NO! You can’t.
- Slides 16-24:
- Repeat the processes above.
Strategy Part 3: Symbolic
Explore equations without blocks to create their equality equations.
- Slide 25:
- Say, “That was a lot of writing! Mathematicians prefer to be as efficient as they can and love to shortform things whenever they can.”
- Slide 26:
- Say, “First of all, a mathematician would use numbers and operations whenever possible. Let’s look at this first example. I am going to read it out loud. Whenever you hear me say a number or operation, stop me and tell me what I should write. Four”
- Write 4.
- Say, “bears…this isn’t a number or operation so we’ll write bears.”
- Write bears.
- Say, “ is the same amount of…” =
- Say, “bears as…again, we’ll write bears.” bears
- Say, “one” 1
- Say, “bag of bears” Write bag of bears.
- Say, “now write this in the handout under Practice Question 1.
- Slide 27:
- Say, “Write out the sentences YOU wrote for the first row using this format.”
- Slides 28-29:
- Repeat this process so that the sentence says “11 bears = 1 bag of bears + 5”
- Slides 30 – 31:
- Say, “This is still more writing than I want to do. We know that this is all about bears so we’ll skip writing the word bears for now. But what single word can I change bag of bears into so that it’s a bit shorter but people still know I’m talking about bears?” Students might say “bag” or “bob” (bag of bears), whatever they say, use that this round.
- Slides 32-33:
- Say, “I bet we can shorten “bag” even more so that I know it’s a bag of bars but I can am writing even less! What could I use?” b
- Slide 34:
- Say, “You’ve been creating some excellent equations. Let’s work backwards from the equation to tell the original story. What would be the story for this equation?” Discuss. 3 bags of bears and 1 on the outside is the same number of bears as 13.
- Say, “Now solve it.” Give time to solve.
- Slide 35:
- Say, “Why did we use b?” to represent bags of bears.
- Ask, “What if I hadn’t brought bags? What if I had brought cups to hide them under? What could I have used?” c
- Ask, “What if I had used suitcases?” s, “In your desk?” d
- Say, “we could have used any letter. Does anyone know what is the most common letter that mathematicians tend to use?” x
- Ask, “What do we have to be careful about with x?” Looks like the multiplication symbol.
- Ask, “What letters do you think mathematicians avoid?” o (Zero), t (addition symbol), L and i (1)
Grade 7
CURRENT Curricular Outcomes:
Model and solve problems, concretely, pictorially and symbolically, problems that can be represented by one-step linear equations of the form x + a = b, where a and b are integers.
Model and solve, concretely pictorially and symbolically, problems that can be represented by linear equations of the form
- ax=b
- ax+b=c
- x/a=b, a not equal to 0
- x/a+b=c, a not equal to 0
where a, b and c are whole numbers
Process of complexity:
In Progress
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- equivalent
- preservation of equality
- equations
- relationship
- expression
- linear equations
- one-step linear equations
Pre-Assessment:
Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student(s) who do not answer MIPI+ Question #1 correctly:
- Complete Strategies from previous grades.
The Process:
Strategy Part 1: Concrete and Part 2: Pictorial (at the same time)
> Introduction
- This activity has been recreated from: http://mrorr-isageek.com/double-clothesline-solving-equations/
Jon Orr has given previous permission to recreate his files.
Materials
- Two long pieces of yarn hung up so that one is above the other.
- Tent Cards
- cut out as tents so that the number/variable is in the front and the blank row is in the back. This will allow them to hang on the yarn.
- Student Practice Questions Handout
- Page Protectors – optional (for students to place handout in)
- Tiny sticky notes work great for students to write numbers on to place on the their “clothesline”.
Instructions
- The Handout has a side with two lines. If you place this in a page protector, students can work right on this during the “together” time. You can also just have them draw two lines on a mini whiteboard.
- The side with Practice questions is done after the class works on questions 1-4 together.
Question 1
- Place 0 on the top number line and 0x on the bottom line so they vertically match.
- Hold up the 3x card and ask “Where should this go? Should it be on the left or the right of zero?”
- Place the 3x on the bottom number line based on where students recommend.
- Say, “I’m placing the 15 right above the 3x and that means equivalence. 3x is the same value as 15.”
- Place 15 on the top line above the 3x.
- Ask, “Where should 9x go?”
- Place on number line based on where students recommend.
- Say, “I want to know what number should be above 9x.”
- Place the ? on the top line above the 9x.
- Have students draw the number lines on their desks and work to figure out the value of 9x.
- Discuss. Possible responses:
- “3 multiplied by 3x is 9x, so 3 multiplied 15 is 45.”
- “If 3x is 15 then one x if 5, so 9x is 45.”
- Place 45.
- Ensure everyone understands both.
- Clear number lines of everything except 0 and 0x.
- Keep the 3x and ? for the next question.
- Create more questions on the spot if needed.
Question 2
- Ask, “Where should I place 3x + 4?”
- Place 3x + 4 on the bottom line.
- Say, “3x + 4 has a value of 16” and 16 on the top line above it.
- Ask, “Where should 3x be placed?”
- Students should see that 3x is less than 3x + 4 so it should go to the left.
- Ask, “What should be the number above?”
- Place the question mark above.
- Give students time to figure out that it should be 12. Place 12.
- Place x.
- Ask, “What must be the value of x?” (4)
- Clear number lines of everything except 0 and 0x.
- Keep the ? for the next question. You will need the 3x again for question 4.
- Create more questions on the spot if needed.
Question 3
- Place x – 3 on the bottom line and 8 on the top line.
- Ask, “Where should x go?”
- After discussion, place x to the right of x-3. This is because “x-3” is referring to the x value subtract 3. So, 3 less than x must be on the left sid eof x.
- Say, “Figure out x.”
- x = 11
- Keep the x for question 4.
- Create more questions on the spot if needed.
Questions to practice
- Give students time to work on the Practice Questions Handout.
Strategy Part 3: Symbolic
Explore equations
- Review the questions you did previously. Record the changes made throughout.
- Write Question 2 on the board: 3x+4 = 16
- Ask, “What did we do first?” Found 3x.
- Ask, “How did we do that?” Shift everything 4 to the left.
- Write “-4” below 3x + 4 and write “-4” below 16.
- Ask, “Where did the bottom row end up?” at 3x.
- Write 3x below the left side.
- Ask, “Where did the top row end up?” at 12
- Write 12 below the right side.
- Ask, “What did we do now?” Find the value of x.
- Ask, “How did we do that?” Divide by 3.
- Say, “We divided 3x by 3.” Write ÷ 3 below 3x.
- Ask, “What else did we divide by 3?” 12
- Write ÷ 3 below 12.
- Ask, “What did we end up with?” x = 4
- Write x = 4 below.
- Repeat for the other questions.
- Write Question 2 on the board: 3x+4 = 16
Grade 8
CURRENT Curricular Outcomes:
Model and solve problems, concretely, pictorially and symbolically, using linear equations of the form
- ax=b
- ax+b=c
- a(x+b)=c
- x/a=b, a not equal to 0
- x/a+b=c, a not equal to 0
where a, b and c are integers
Process of complexity:
Start with positive coefficients and addition statements. When students demonstrate understanding, proceed with positive coefficients and subtraction statements. When students demonstrate understanding, proceed with negative coefficients and addition statements. When students demonstrate understanding, proceed with negative coefficients and subtraction statements.
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- two-variable linear relations
- linear equations
- congruence
- relationship
Pre-Assessment:
Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student(s) who do not answer MIPI+ Question #1 correctly:
- Complete Strategies from previous grades.
The Process:
Strategy Part 1: Concrete and Part 2: Pictorial (at the same time)
> Introduction
- This activity has been recreated from: http://mrorr-isageek.com/double-clothesline-solving-equations/
Jon Orr has given previous permission to recreate his files.
- This activity has been created as a Desmos activity: Super Secret Spy Mission.
Materials
- Two long pieces of yarn hung up so that one is above the other.
- Tent Cards
- cut out as tents so that the number/variable is in the front and the blank row is in the back. This will allow them to hang on the yarn.
- Student Practice Questions Handout
- Page Protectors – optional (for students to place handout in)
- Tiny sticky notes work great for students to write numbers on to place on the their “clothesline”.
Instructions
- The Handout has a side with two lines. If you place this in a page protector, students can work right on this during the “together” time. You can also just have them draw two lines on a mini whiteboard.
- The side with Practice questions is done after the class works on questions 1-4 together.
Question 1
- Place 0 on the top number line and 0x on the bottom line so they vertically match.
- Hold up the 3x card and ask “Where should this go? Should it be on the left or the right of zero?”
- Place the 3x on the bottom number line based on where students recommend.
- Say, “I’m placing the 15 right above the 3x and that means equivalence. 3x is the same value as 15.”
- Place 15 on the top line above the 3x.
- Ask, “Where should 9x go?”
- Place on number line based on where students recommend.
- Say, “I want to know what number should be above 9x.”
- Place the ? on the top line above the 9x.
- Have students draw the number lines on their desks and work to figure out the value of 9x.
- Discuss. Possible responses:
- “3 multiplied by 3x is 9x, so 3 multiplied 15 is 45.”
- “If 3x is 15 then one x if 5, so 9x is 45.”
- Place 45.
- Ensure everyone understands both.
- Clear number lines of everything except 0 and 0x.
- Keep the 3x and ? for the next question.
- Create more questions on the spot if needed.
Question 2
- Ask, “Where should I place 3x + 4?”
- Place 3x + 4 on the bottom line.
- Say, “3x + 4 has a value of 16” and 16 on the top line above it.
- Ask, “Where should 3x be placed?”
- Students should see that 3x is less than 3x + 4 so it should go to the left.
- Ask, “What should be the number above?”
- Place the question mark above.
- Give students time to figure out that it should be 12. Place 12.
- Place x.
- Ask, “What must be the value of x?” (4)
- Clear number lines of everything except 0 and 0x.
- Keep the ? for the next question. You will need the 3x again for question 4.
- Create more questions on the spot if needed.
Question 3
- Place x – 3 on the bottom line and 8 on the top line.
- Ask, “Where should x go?”
- After discussion, place x to the right of x-3. This is because “x-3” is referring to the x value subtract 3. So, 3 less than x must be on the left sid eof x.
- Say, “Figure out x.”
- x = 11
- Keep the x for question 4.
- Create more questions on the spot if needed.
Question 4
- Place 5x-2 on the bottom line and 33 on the top line.
- Ask, “Where should 5x go?”
- After discussion, place 5x to the right of 5x-2
- Give students time to figure out the rest to solve for x.
- 5x = 35
- x = 7
- Discuss. You can place x on the bottom line to help. You can place 7 on the line after discussion.
- Clear the lines except for 0 and 0x.
- Keep the x for question 5.
- Create more questions on the spot if needed.
Question 5
- Place 3x+14 on the bottom line and 2 on the top line.
- Ask, “Where should we place 3x?”
- Give lots of time for student discussion. Students may want to put it in between 0x and 3x+14.
- It actually needs to be placed 14 down from 3x+14 and 2. 14 down from 2 is -12.
- Ask students to figure out x. (-4)
- Create more questions on the spot if needed.
Questions to practice
- Give students time to work on the Practice Questions Handout.
Challenge Questions
- 4x + 10 = 6x + 2
- One way is to figure out where x would be on the top row.
- 10 = 2x+2
- 8=2x
- 4=x
- -2x + 4 = -2
- -2x = 6
- -x = -3
- x = 3
- One way is to figure out where x would be on the top row.
- -3x + 42 = 12
- -3x = -30
- -x = -10
- x = 10
- -4x – 3 = 5
- -4x = 8
- -x = 2
- x = -2
Strategy Part 3: Symbolic
Explore equations
- Review the questions you did previously. Record the changes made throughout.
- Write Question 2 on the board: 3x+4 = 16
- Ask, “What did we do first?” Found 3x.
- Ask, “How did we do that?” Shift everything 4 to the left.
- Write “-4” below 3x + 4 and write “-4” below 16.
- Ask, “Where did the bottom row end up?” at 3x.
- Write 3x below the left side.
- Ask, “Where did the top row end up?” at 12
- Write 12 below the right side.
- Ask, “What did we do now?” Find the value of x.
- Ask, “How did we do that?” Divide by 3.
- Say, “We divided 3x by 3.” Write ÷ 3 below 3x.
- Ask, “What else did we divide by 3?” 12
- Write ÷ 3 below 12.
- Ask, “What did we end up with?” x = 4
- Write x = 4 below.
- Repeat for the other questions.
- Write Question 2 on the board: 3x+4 = 16
Grade 9
CURRENT Curricular Outcomes:
In Progress
Process of complexity:
In Progress
Key Vocabulary:
The following key vocabulary should be used with and by students. Key Vocabulary will be italicized every time it is used below in order to draw attention to its introduction and use.
- In Progress
Pre-Assessment:
> Administer MIPI+ Question #1
- Find out more about administering and assessing the MIPI+ Question #1.
> Student(s) who do not answer MIPI+ Question #1 correctly:
- Complete Kindergarten Strategy Part 1 as a class using between 6-10 objects
- Identify which students know without counting that moving the objects doesn’t change the count.
- You may need to repeat previous strategies with individual students to identify specifically where they are struggling.
The Process:
Strategy Part 1: Concrete
> Introduction
- In progress
Strategy Part 2: Pictorial
> Introduction
- In progress
Strategy Part 3: Symbolic
Explore equations
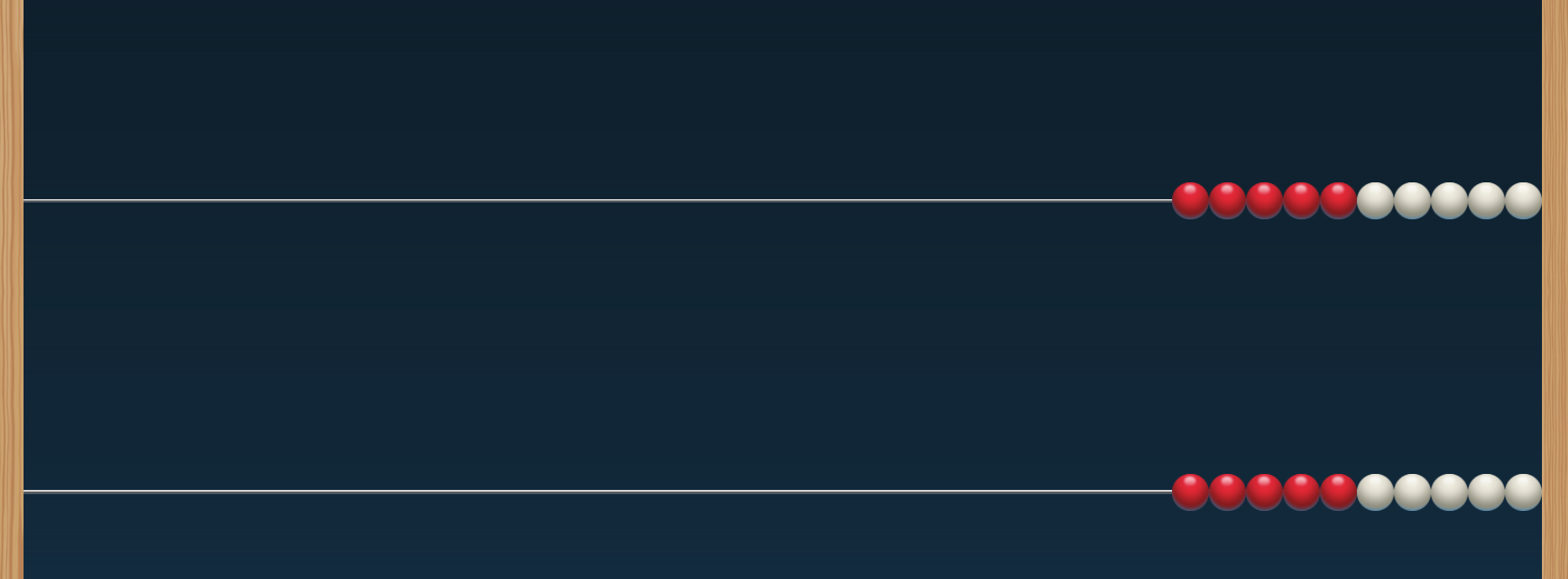
- Use store bought, homemade or virtual rekenreks to explore equality with beads.
- Students can compare different ways that you can make 10, representing them using the equation format as above. 4 + 6 = 5 + 5. ie. “To move ten over, I moved 4 and then 6: 4 + 6; Breanne moved 3 and then 7: 3+7; We both moved ten over.”
- When you want to work with numbers other than 10, such as 9, just move 9 over slightly so that and then work from there.
- Want to work with numbers higher than 10? Add more rekenrek rows.
How do the connections we make with rekenreks strengthen our relational understanding of the equal sign?

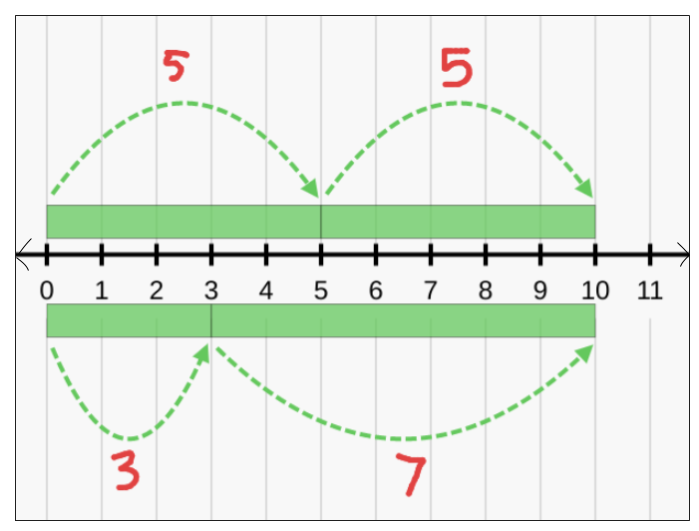
- Number lines allow you to show “jumps” to get to a number. For example, the numberline on the right shows 5 + 5 on the top is the same as 3 + 7 on the bottom. They both get to the same answer of 10.
- Open number lines would be the next step in understanding. Students wouldn’t show the individual tick marks nor the numbers in between 0 and 10.
- When working with number lines. ensure that you are drawing arrows at each end. Numberlines do not start and end at a specific number. (See the image on the right)
How do the connections we make with number lines strengthen our relational understanding of the equal sign?
Where is this going?
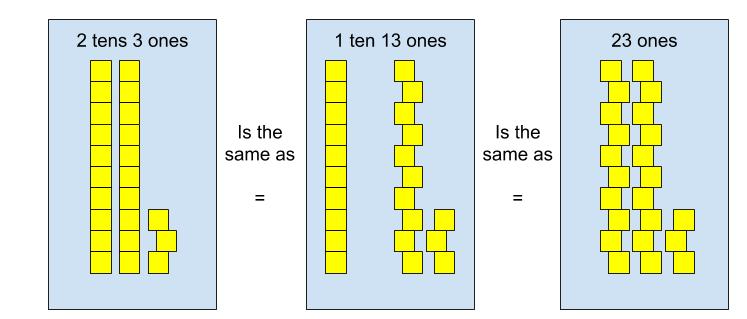
Place Value:
Students’ understanding of equality has a huge impact on place value. How many different ways are there to represent the number 23 using base ten blocks?
Solving Algebraic Equations:
Students’ understanding of equality has a huge impact on their algebraic thinking. Why is it that “what you do to one side…you must do to the other”?
The Commutative Property:
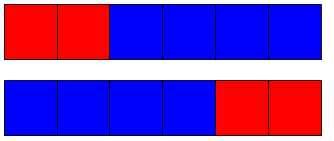
Addition: Changing the order of addends does not change the sum.
Simplified: Numbers can be added in any order: 2 + 4 is the same as 4 + 2
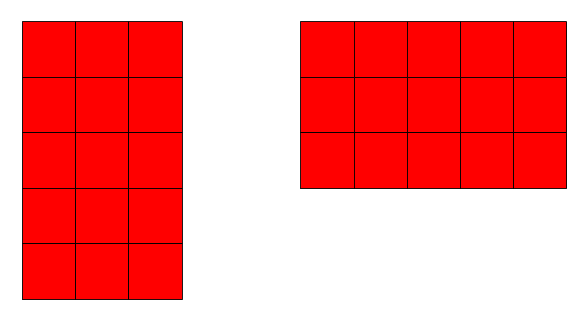
Multiplication: Changing the order of factors does not change the product.
Simplified: Numbers can be multiplied in any order: 3 x 5 is the same as 5 x 3
This property is not applicable to subtraction or division.
2 – 4 is not the same as 4 – 2.
3 divided by 5 is not the same as 5 divided by 3.




